Schreiber Super Lie n-algebra of Super p-branes
The following are a couple of related talks that I have given.
Expository talk notes are below. For more detailed lecture notes see: geometry of physics – fundamental super p-branes. For related talk notes see Super p-Brane Theory emerging from Super Homotopy Theory and Super topological T-Duality.
-
Super Lie -algebra of Super -branes
talks at
Fields, Strings, and Geometry Seminar, Surrey, 5th-9th Dec. 2016
Abstract. It is “well known” that the Green-Schwarz sigma models for the superstring and the membrane are higher super-WZW-type models classified by super Lie algebra cohomology in degree 3 and 4, respectively. I will explain that if one passes instead to super Lie -algebras, then the entire brane content of string/M-theory is derivable from the homotopy theory of higher super Lie algebras, as are the pertinent dualities (HET/M/IIA/IIB/F) and various fine details, such as the twisted K-theory of RR-charges and the local structure of super T-folds (doubled super-spacetimes). This is based on arXiv:1611.06536, which is joint with D. Fiorenza, H. Sati, as well as on work with J. Huerta.
-
Duality in String/M-Theory from Cyclic cohomology of Super Lie -algebras
talk at
Topological Quantum Field Theory Seminar, Lisbon, 20th Jan 2017 (alongside Iberian Strings 2017), Lisbon, 20. Jan 2017
Open problem:
Understand M-theory from first principles, not via perturbative string theory.
Theorem reviewed here:
Much of the known/expected structure of M-theory
follows from analysis of the superpoint
in super Lie n-algebra homotopy theory.
Based on Fiorenza-Sati-Schreiber 13, 16a, 16b.
If history is a good guide, then we should expect that anything as profound and far-reaching as a fully satisfactory formulation of M-theory is surely going to lead to new and novel mathematics. Regrettably, it is a problem the community seems to have put aside - temporarily. But, ultimately, Physical Mathematics must return to this grand issue. (G. Moore, p. 45 of “Physical Mathematics and the Future”, talk at Strings 2014)
Contents
Spacetime
Everything we say below follows
by developing this elementary phenomenon (highlighted in Schreiber 15):
Proposition
Consider the superpoint
regarded as an abelian super Lie algebra.
Its maximal central extension is
the super-worldline of the superparticle:
-
whose even part is spanned by one generator
-
whose odd part is spanned by one generator
-
the only non-trivial bracket is
Then consider the superpoint
Its maximal central extension is
the , super Minkowski spacetime
-
whose even part is , spanned by generators
-
whose odd part is , regarded as
the Majorana spinor representation
of
-
the only non-trivial bracket is the spinor bilinear pairing
where is the charge conjugation matrix.
Proof
Recall that
-dimensional central extensions of super Lie algebras
are classified by 2-cocycles.
These are super-skew symmetric bilinear maps
satisfying a cocycle condition.
The extension that this classifies
has underlying super vector space
the direct sum
an the new super Lie bracket is given
on pairs
by
The condition that the new bracket satisfies the super Jacobi identity
is equivalent to the cocycle condition on .
Now
in the case that ,
then the cocycle condition is trivial
and a 2-cocycle is just a symmetric bilinear form
on the fermionic dimensions.
So
in the case
there is a unique such, up to scale, namely
But
in the case
there is a 3-dimensional space of 2-cocycles, namely
If this is identified with the three coordinates
of 3d Minkowski spacetime
then the pairing is the claimed one
(see at supersymmetry – in dimensions 3,4,6,10).
This phenomenon continues:
Theorem
The diagram of super Lie algebras shown on the right
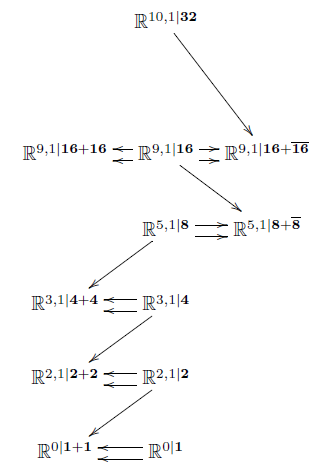
is obtained by consecutively forming
maximal central extensions
invariant with respect to
the maximal subgroup of automorphisms
for which there are invariant cocycles at all.
Here
is the , super-translation supersymmetry algebra.
And these subgroups are
the spin group covers
of the Lorentz groups .
Side remark: That every super Minkowski spacetime is some central extension of some superpoint is elementary. This was highlighted in (Chryssomalakos-Azcárraga-Izquierdo-Bueno 99, 2.1). But most central extensions of superpoints are nothing like super-Minkowksi spacetimes. The point of the above proposition is to restrict attention to iterated invariant central extensions and to find that these single out the super-Minkowski spacetimes.
Conclusion:
Just from studying iterated invariant central extensions
starting with the superpoint,
we (re-)discover
May we extend further?
Branes
There are no further invariant 2-cocycles on 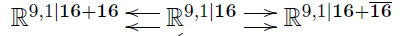
But there is an invariant 3-cocycle.
There are no further invariant 2-cocycles on
But there is an invariant 4-cocycle.
So:
What are higher super Lie algebra cocycles?
And what kind of extensions do they classify?
Quick answer:
Higher cocycles are closed elements in a Chevalley-Eilenberg algebra.
They classify super Lie-∞ algebra extensions.
This we explain now.
Definition
For a super Lie algebra
its Chevalley-Eilenberg algebra
is the super-Grassmann algebra on the dual super vector space
equipped with a differential
that on generators is the linear dual of the super Lie bracket
and which is extended to
by the graded Leibniz rule (i.e. as a graded derivation).
Here all elements are -bigraded,
the first being the cohomological grading in ,
the second being the super-grading (even/odd).
The sign rule is
A -cocycle on
is an element of degree in
which is closed. It is non-trivial if it is not -exact.
We may think of equivalently
as the dg-algebra of left-invariant super differential forms
on the corresponding simply connected super Lie group .
Example
For
and a real spin representation of
the super-translation supersymmetry super Lie algebra
has Chevalley-Eilenberg algebra generated by
-
in bi-degree ;
-
in bi-degree .
with differential
where
is the standard spinor bilinear pairing
in the spin representation .
If we think of super Minkowski spacetime
as the supermanifold with
-
even coordinates ;
-
odd coordinates
then these generators correspond to these super differential forms:
the super-vielbein.
Notice that alone
fails to be a left invariant differential form,
in that it is not annihilated by the supersymmetry
vector fields
Therefore the all-important correction term above.
Example
The 2-cocycle that classifies the extension
is
Regarded as a 2-form on ,
this is the curvature of the WZW-term
in the Green-Schwarz sigma-model for the D0-brane.
See below.
Proposition
(Achúcarro-Evans-Townsend-Wiltshire 87, Brandt 12-13)
The maximal invariant 3-cocycle on 10d super Minkowski spacetime is
This is the WZW term for the Green-Schwarz superstring (Green-Schwarz 84).
The maximal invariant 4-cocycle on super Minkowski spacetime is
This is the higher WZW term for the supermembrane (Bergshoeff-Sezgin-Townsend 87).
This classification is also known as
the old brane scan.
Here “higher WZW term” means the following:
Regard
as a left invariant differential form
Choose any differential form potential
i.e. such that
(This will not be left-invariant.)
Then the Green-Schwarz action functional for the superstring
is the function on the space of sigma-model fields
(morphisms of supermanifolds)
given by
The first term is the Nambu-Goto action
the second is a WZW term.
Originally Green-Schwarz 84 introduced
to ensure an additional fermionic symmetry: “kappa-symmetry”.
Notice that looks somewhat complicated
and is not unique.
That it is simply a WZW-term
for the supersymmetry supergroup
was observed in Henneaux-Mezincescu 85.
Similarly,
choose any differential form potential such that
(This will not be left-invariant.)
Then the Green-Schwarz type action functional
for the supermembrane
is the function on sigma-model fields
given by
On the right this is
the higher WZW term.
Now we discuss that higher cocycles classify higher extensions:
First observe that
Proposition
Homomorphisms of super Lie algebras
are in natural bijection with the homomorphisms of dg-algebras
between their Chevalley-Eilenberg algebra, going the opposite direction:
This means that we may identify super Lie algebras with their CE-algebras.
In the terminology of category theory: the functor
given by
is fully faithful.
Therefore it is natural to make the following definition.
Definition
A super Lie-infinity algebra of finite type is
-
a -graded super vector space
degreewise of finite dimension
-
for all a multilinear map
of degree
such that
the graded derivation on the super-Grassmann algebra given by
squares to zero:
and hence defines a dg-algebra
A homomorphism of super -algebras is dually a homomorphism of their CE-algebras.
If is concentrated
in degrees to
we call it a super Lie n-algebra.
Side remark:
We may drop the assumption of degreewise finiteness
by regarding as a free graded co-commutative coalgebra
and as a differential
making a differential graded coalgebra.
-algebras in the sense of def. were introduced in Lada-Stasheff 92.
That they are fully characterized
by their Chevalley-Eilenberg dg-(co-)algebras
is due to Lada-Markl 94.
See Sati-Schreiber-Stasheff 08, around def. 13.
But in fact the CE-algebras of super -algebras of finite type
were implicitly introduced
as tools for the higher super Cartan geometry of supergravity
already in D’Auria-Fré 82 (see D'Auria-Fré formulation of supergravity)
where they were called FDAs.
| higher Lie theory | supergravity |
|---|---|
| super Lie n-algebra | “FDA” |
However,
what has not been used in the “FDA” literature
is that -algebras are objects in homotopy theory:
Proposition
There exists a model category such that
-
its fibrant objects are the (super-)L-∞ algebras
with the above homomorphisms between them;
-
and
-
the weak equivalences between (super-)-algebras are the quasi-isomorphisms;
-
fibrations between (super-)-algebras are the surjections
on the underlying chain complex (using the unary part of the differential).
-
For more see at model structure for L-infinity algebras.
Concretely,
this implies in particular that
every homomorphisms of super L-∞ algebras
is the composite of a quasi-isomorphism followed by a surjection
That surjective homomorphism
is called a fibrant replacement of .
Definition
Given homomorphisms of super L-∞ algebras
then its homotopy fiber
is the kernel of any fibrant replacement
Standard facts in homotopy theory assert
that is well-defined
up to quasi-isomorphism.
See at Introduction to homotopy theory – Homotopy fibers.
Proposition
(Fiorenza-Sati-Schreiber 13, theorem 3.8)
Write
for the line Lie (p+2)-algebra, given by
A -cocycle on an -algebra is equivalently a homomorphim
The homotopy fiber of this map
is given by adjoining to a single generator
forced to be a potential for :
Conclusion.
The higher central extensions
classified by higher cocycles
are their homotopy fibers.
This way we may finally continue
the progression of invariant central extensions
to higher central extensions:
Definition
Name the homotopy fibers of the cocycles
which are the higher WZW terms
of the superstring and the supermembrane
as follows
The super Lie 2-algebra is given by
This is a super-version of the string Lie 2-algebra (Baez-Crans-Schreiber-Stevenson 05
which controls Green-Schwarz anomaly cancellation (Sati-Schreiber-Stasheff 12)
and the topology of the supergravity C-field (Fiorenza-Sati-Schreiber 12a, 12b).
The membrane super Lie 3-algebra is given by
This dg-algebra was first considered in D’Auria-Fré 82 (3.15)
as a tool for constructing 11-dimensional supergravity.
For exposition from the point of view of Lie 3-algebras see also Baez-Huerta 10.
Hence the progression
of maximal invariant extensions of the superpoint
continues as a diagram
of super L-∞ algebras like so:
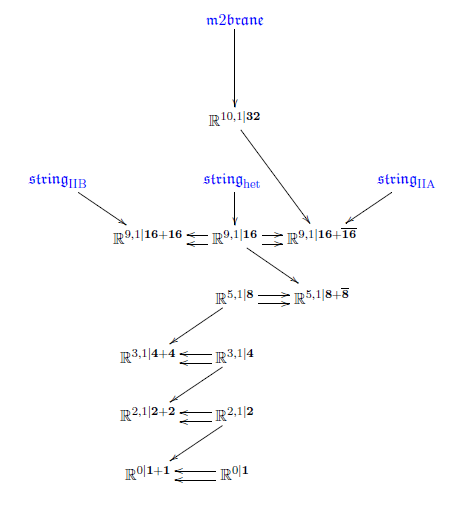
(While every extension displayed is a maximal invariant higher central extension, not all invariant higher central extensions are displayed. For instance there are string and membrane GS-WZW-terms / cocycles also on the lower dimensional super-Minkowski spacetimes (“non-critical”), e.g. the super 1-brane in 3d and the super 2-brane in 4d.)
The “old brane scan” ran into a conundrum:
Given that superstrings and supermembranes
are nicely classified by super Lie algebra cohomology
why do the other super p-branes not show up similarly?
Where are the D-branes and the M5-brane?
But now we see that we should look for
further higher cocycles
not on super Lie algebras
but on super L-∞ algebras.
Proposition
(Chryssomalakos-Azcárraga-Izquierdo-Bueno 99, Sakaguchi 99, Fiorenza-Sati-Schreiber 13)
The higher WZW terms for the D-branes
are invariant super -cocycles
on the higher extended super Minkowski spacetimes from above
Similarly,
the higher WZW term for the M5-brane
is an invariant super 7-cocycle
of the form
By the above, these cocycles classify
further higher super -algebra extensions
Notice that all these are higher cocycles
except for that of the D0-brane, which is just a 2-cocycle.
The ordinary central extension that this classifies
is just that which grows the 11th M-theory dimension by the above example .
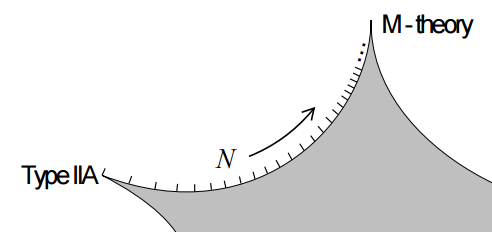
This may be thought of
as a super -theoretic incarnation
of D0-brane condensation
In conclusion:
by forming
iterated (maximal) invariant higher central super -extensions
of the superpoint,
we obtain the following “brane bouquet”
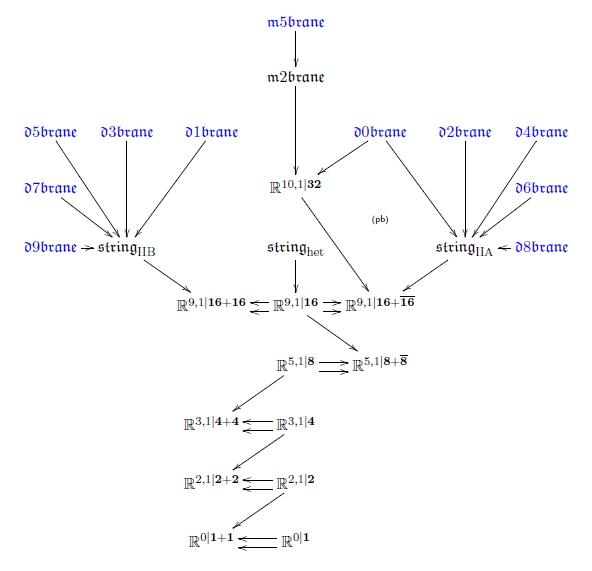
Each object in this diagram of super L-∞ algebras
is a super spacetime or super p-brane of string theory / M-theory.
Moreover, this diagram knows the brane intersection laws:
there is a morphism
precisely if the given species of -branes may end on the given species of -branes
(more discussion of this is in Fiorenza-Sati-Schreiber 13, section 3).
Perhaps we need to understand the nature of time itself better. One natural way to approach that question would be to understand in what sense time itself is an emergent concept, and one natural way to make sense of such a notion is to understand how pseudo-Riemannian geometry can emerge from more fundamental and abstract notions such as categories of branes. (G. Moore, p.41 of “Physical Mathematics and the Future”, talk at Strings 2014)
But how are we to think of the extended super Minkowski spacetimes geometrically?
This is clarified by the following result:
Proposition
(Fiorenza-Sati-Schreiber 13, section 5)
Write for the super 2-group
that Lie integrates the super Lie 2-algebra
subject to the condition that it carries a globally defined Maurer-Cartan form.
Then for a worldvolume smooth manifold
there is a natural equivalence
between “higher Sigma-model fields”
and pairs, consisting of
an ordinary sigma-model field
and a gauge field on the worldvolume of the D-brane
twisted by the Kalb-Ramond field.
This is the Chan-Paton gauge field on the D-brane.
Similarly:
Write for the super 3-group
that Lie integrates the super Lie 3-algebra
subject to the condition that it carries a globally defined Maurer-Cartan form.
Then for a worldvolume smooth manifold
there is a natural equivalence
between “higher Sigma-model fields”
and pairs, consisting of
an ordinary sigma-model field
and a higher gauge field on the worldvolume of the M5-brane
and twisted by the supergravity C-field.
(See also at Structure Theory for Higher WZW Terms, session II).
In conclusion this shows that
given a cocycle for some super -brane species
inducing an extended super Minkowski spacetime via its homotopy fiber
and then given a consecutive cocycle for a -brane species on that homotopy fiber
then -branes may end on -branes
and the -branes propagating in the extended spacetime
see a higher gauge field on their worldvolume
of the kind sourced by boundaries of -branes.
Hence the extended super Minkowski spacetime
is like the original super spacetime
but filled with a condensate of -branes
whose boundaries source a higher gauge field.
While this is good,
it means that at each stage of the brane bouquet
we are describing -brane dynamics
on a fixed -brane background field.
But more generally
we would like to describe the joint dynamics
of all brane species at once.
This we turn to now.
Fields
We now discuss that
There is homotopy descent of -brane WZW terms
from extended super Minkowski spacetime
down to ordinary super Minkowski spacetime
which yields cocycles in twisted cohomology
for the RR-field and the M-flux fields.
(Fiorenza-Sati-Schreiber 15, 16a).
In order to explain this we now first recall
the general nature of twisted cohomology
and its role in string theory.
Twisted generalized cohomology
It is often stated that a
Chan-Paton gauge field on coincident D-branes
is an SU(n)-vector bundle ,
hence a cocycle in nonabelian cohomology in degree 1.
But this is not quite true.
In general there are D-branes and anti-D-branes coinciding,
carrying Chan-Paton gauge fields
(of rank ) and (of rank ), respectively,
yielding a pair of vector bundles
Such pairs are also called virtual vector bundles.
But D-branes annihilate with anti-D-branes (Sen 98)
when they have exact opposite D-brane charge,
which here means that they carry the same Chan-Paton vector bundle.
In other words, pairs as above of the special form
are equivalent to pairs of the form .
Hence the net Chan-Paton charge of coincident branes and anti-branes
is the equivalence class of
under the equivalence relation which is generated by the relation
for all complex vector bundles (Witten 98, Witten 00).
The additive abelian group of such equivalence classes of virtual vector bundles
is called topological K-theory.
This behaves in many ways as ordinary cohomology does, but is richer.
One says that it is a generalized cohomology theory.
It follows that also the RR-fields are in K-theory (Moore-Witten 00).
Topological K-theory is similar to ordinary cohomology
but is a generalized (Eilenberg-Steenrod) cohomology theory.
A generalized cohomology theory is represented by a spectrum
(in the sense of stable homotopy theory):
A spectrum is a sequence of pointed topological spaces
equipped with weak homotopy equivalences
from one to the loop space of the next.
Given this, then the -cohomology of any topological space is
For topological K-theory one writes
with
with the stable unitary group,
and the classifying space for complex vector bundles.
But above we saw
that the Chan-Paton gauge field on a D-brane
is actually a twisted vector bundle
with twist given by the Kalb-Ramond field
sourced by a string condensate.
(Freed-Witten anomaly cancellation)
Such twisted cohomology generalized cohomology is given by
-
a classifying space of twists
-
a spectrum object in the slice category , namely a sequence of spaces equipped with maps
and weak equivalences
Extremal examples:
-
an ordinary spectrum
is a parameterized spectrum over the point;
-
an ordinary space
is identified with the zero-spectrum parameterized over :
Then
-
a twist for -cohomology of is a map
-
the -twisted -cohomology of is
There is a homotopy fiber sequence (in parameterized spectra)
and this equivalently exhibits as the homotopy quotient of an ordinary spectrum by a -infinity-action.
(Nikolaus-Schreiber-Stevenson 12, section 4.1)
Assume that is simply connected, i.e. of the form .
We now translate this situation to super L-∞ algebras
via the central theorem of rational homotopy theory.
Rational homotopy theory
On every loop space ,
the operation of concatenation of loops
gives the structure of a group up to coherent higher homotopy
called a “grouplike A-∞ space”
or ∞-group for short.
Conversely, for an ∞-group
there is an essentially unique connected space
with .
Every double loop space
becomes a “first order abelian” ∞-group
by exchanging loop directons
called a braided ∞-group,
For a braided ∞-group then
is itself an ∞-group
and so there exists an essentially unique simply connected space
with
And so forth:
Every triple loop space
becomes a “second order abelian” ∞-group
by exchanging loop directons
called a sylleptic ∞-group.
etc.
In a spectrum ,
the maps
exhbit as an infinite loop space
hence as a fully abelian ∞-group.
It turns out that by a homotopy theoretic version of Lie theory,
there is an L-∞ algebra associated with any ∞-group
or
etc.
Its Chevalley-Eilenberg algebra
is called a Sullivan model for .
For example the -algebra associated with an Eilenberg-MacLane space
is the line Lie-n algebra from above:
The main theorem of rational homotopy theory (Quillen 69, Sullivan 77)
says that the L-∞ algebra equivalently reflects the rationalization of
(in fact the real-ification, since we are considering -algebras over the real numbers).
This means that weak equivalence between -algebras correspond to maps between spaces
that induce isomorphism on real-ified homotopy groups
For concise review in the language that we use here see Buijs-Félix-Murillo 12, section 2.
We apply this rational homotopy theory functor
to find the -algebraic version of parameterized spectra
hence of twisted cohomology:
Here is a chain complex
underlying the real-ification of the spectrum
(stable Dold-Kan correspondence).
So for some super Minkowski spacetime, a cocycle in -twisted -cohomology is a diagram of the form
Now given one stage in the brane bouquet
we want to descent to .
By the general theory of principal ∞-bundles (Nikolaus-Schreiber-Stevenson 12):
-
has a -∞-action
-
equipping with an -∞-action
is equivalent to finding a homotopy fiber sequence as on the right here:
-
is -equivariant precisely if it descends to a morphism
-
if so, then resulting triangle diagram
exhibits as a cocycle in (rational) -twisted cohomology
with respect to the local coefficient bundle .
We now work out this general prescription
for the cocycles in the brane bouquet.
RR-fields
By the brane bouquet above
the type IIA D-branes
are given by super cocycles of the form
for .
Notice that
has one generator in each even degree, the universal Chern classes.
Hence the -algebra
is given by
This allows to unify the D-brane cocycles
into a single morphism of super -algebras of the form
By the above prescription, descending is equivalent
to finding a commuting diagram in the homotopy category of super -algebras
of the form
This turns out to exist as follows (Fiorenza-Sati-Schreiber 16a, section 5):
Define the -algebra
by
Moreover write
for the super -algebra whose Chevalley-Eilenberg algebra is
Proposition
(Fiorenza-Sati-Schreiber 16a, theorem 4.16)
The super -algebra
is a resolution of type IIA super-Minkowski spacetime.
in that there is a weak equivalence
This fits into a commuting diagram of the form
In conclusion
the type IIA F1-brane and D-brane cocycles with -coefficients
do descent to super-Minkowski spacetime
as one single cocycle with coefficients
in rationalized twisted K-theory.
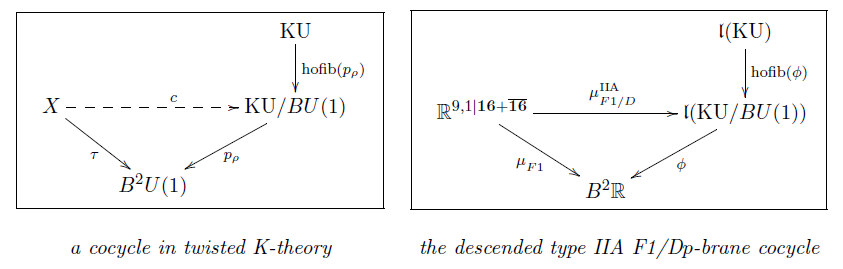
M-flux fields
The part of the brane bouquet giving the M-branes is
In order to descend this, consider the -algebra corresponding to the 4-sphere
By standard results on rational n-spheres, this is given by
Proposition
Fiorenza-Sati-Schreiber 15, section 3
There is a homotopy fiber sequence of -algebras as on the right
which is the image under of the quaternionic Hopf fibration.
This makes a commuting diagram
in the homotopy category of super -algebas
of the form
In conclusion
this says that, rationally,
M2-brane charge is in degree-4 ordinary cohomology
and it twists M5-brane charge
which is, rationally, in unstable degree-4 cohomotopy.
This confirms a conjecture due to
(Sati 10, section 6.3, Sati 13, section 2.5).
based on the observation that
the equations of motion of 11-dimensional supergravity
for the supergravity C-field field strength say that
with the Hodge dual
and this is just the algebraic relation for the Sullivan model of the rational 4-sphere.
Notice that, unstably, the 4-sphere
is just the space whose non-torsion homotopy groups
hence those that are visible in rational homotopy theory
are in degrees 2+2 and 5+2:
| k | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
But the correct non-rational lift of the -coefficients
will also have to be such that it somehow gives rise to twisted K-theory
under double dimensional reduction. This is still an open problem.
For further comments see the talk
Equivariant cohomology of M2/M5-branes
Now that we have found
the descended -cocycles
for all super -branes
in twisted cohomology, rationally,
we may analyze their behaviour under double dimensional reduction
and discover the super -algebraic incarnation
of various dualities in string theory.
Double dimensional reduction
Underlying most of the dualities in string theory is
the phenomenon of double dimensional reduction
so called because:
-
the dimension of spacetimes is reduced
by Kaluza-Klein compactification on a fiber ;
-
in parallel the dimension of branes is reduced
if they wrap .
For example double dimensional reduction is supposed to underly
the duality between M-theory and type IIA string theory:
-
spacetime is an 11d circle-fiber bundle
locally of the form
over a 10d base spacetime;
-
an M-theory membrane (M2-brane) with cyclindrical worldvolume
wraps the circle fiber if its trajectory
is of the form
As the Riemannian circumference of the circle fiber tends towards zero
this effectively looks like the 2-dimensional worldsheet of a string
tracing out a trajectory in 10-dimensional spacetime:
But there is also “single dimensional reduction”
when the membrane does not wrap the fiber space:
In this case it looks like a membrane in 10d spacetime,
now called the D2-brane.
Similarly the M5-brane in M-theory
to yield a 4-brane in 10d, called the D4-brane
or it may not wrap the circle fiber
to yield a 5-brane in 10d, called the NS5-brane.
Beware the naive treatment of branes in this traditional argument.
And even naively, this is not the full story yet:
The -fibration itself is supposed to re-incarnate in 10d
as the D0-brane and the D6-brane.
Hence double dimensional reduction from M-theory to type IIA string theory
is meant to, schematically, involve decompositions as follows
Above we saw that all super p-branes are
characterized by the flux fields that they are charged under,
more precisely by the bispinorial component of
which is constrained to be super-tangent-space-wise the form
where is the super vielbein (graviton and gravitino).
Hence we will formalize double dimensional reduction in terms of these fields.
Again there is a naive picture to help the intuition:
Let be the differential 4-form flux field strength of the supergravity C-field.
Under the Gysin sequence for the spherical fibration
this decomposes in cohomology as
thus giving rise in 10d to
-
a 3-form , the Kalb-Ramond B-field field strength that the string couples to;
-
a 4-form , the RR-field field strength in degree 4, that the D2-brane couples to.
Similary the 7-form field strength decomposes as
thus giving rise in 10d to
-
a 6-form , the RR-field field strength in degree 6, that the D4-brane couples to
-
a 7-form , the dual NS-NS field strength that the NS5-brane couples to.
The advantage of this perspective on double dimensional reduction
from the point of view of the background flux fields
is that powerful tools from cohomology theory apply.
To first approximation
background fluxes represent classes in ordinary cohomology (their charges).
There is a classifying space for ordinary cohomology
(called an Eilenberg-MacLane space, often denoted ).
Hence the charge of /-flux, to first approximation, is represented by a classifying map
and we saw that under double dimensional reduction
this is supposed to transmute into a map of the form
Which mathematical operation could cause such a transmutation?
We will now find such an operation
and then use it to give an improved definition of double dimensional reduction,
one that knows about all the fine print of brane charges.
Via free looping (no 0-brane effect)
Let’s first record formally
what was going on in the above story.
In the above double dimensional reduction
of the naive M-fluxes on a trivial 11d circle bundle
we used
-
the Cartesian product with the circle
-
functions out of the circle.
Let’s have a closer look at these two operations:
It is a classical fact about locally compact topological spaces
(which includes all topological spaces that one cares about in physics)
that
given topological spaces , and , then there is a natural bijection
where
-
is the product topological space of with
(the set of pairs of points euipped with the product topology)
-
is the mapping space from to ,
(the set of continuous functions) equipped with the compact-open topology)
Except for the subtlety with the topology
this bijection is just rewriting
a function of two variables as a function with values in a second function
One says that the two functors
form a adjoint pair or an adjunction.
A remarkable amount of structure comes with every adjunction:
-
generally called the unit of the adjunction,
here is the wrapping operation
-
generally called the counit of the adjunction,
here is the evaluation map
that evaluates a function on an argument
We will see now that the following general fact
about adjoint functors
serves to implement the above physics story
of wrapped branes:
Fact.
The adjunct of a map of the form
is the composite of its image under with the adjunction unit :
Moreover, we will see that the following generall fact in homotopy theory
accurately implements the idea of dimensional reduction of the brane dimensions:
For the circle, then
is also called the free loop space of .
Proposition
For a general topological group, then its free loop space
is weakly homotopy equivalent to the
homotopy quotient of by its adjoint action.
In the special case that is an abelian topological group.
then this becomes a weak homotopy equivalence of following simple form
This captures the required reduction on brane dimension!
In particular if then
Example
Consider naive -flux fields and
on an 11d spacetime that is a trivial circle bundle .
Its charges is represented by a map of the form
By adjunction this is identified with a map of the form
where on the right we have the transmuted coefficients by prop.
This is exactly the result we were after.
Better yet, the adjunction yoga
accurately reflects the physics story:
For consider a -brane propagating in 10d spacetimes along a trajectory
and coupled to these dimensionally reduced background fields
By adjunction this is identified with a map of the form
and this is exactly the coupling we saw in the story of double dimensional reduction.
So this works well as far as it goes, but
so far it only applies to trivial circle fibrations
and it does not see the D0-charge.
We now disucss the improvement to the full formulation.
Via cyclification (with 0-brane effects)
In general the M-theory circle bundle
is only locally a product with of with .
For example
the complement of the locus of a KK-monopole spacetime
is a circle principal bundle with first Chern class
equal to the charge carried by the KK-monopole.
(which is the corresponding number of coincident D6-branes in type IIA).
Hence in general the above formulation of double dimensional reduction
via the pair of adjoint functors
works only locally.
But the problem to be solved is easily identified:
Essentially by definition, in a circle principal bundle
the fibers may all be identified with a fixed abstract circle
only up to rigid rotation.
Hence while in general the above wrapping-map
given by sending each point of to its fiber “wrapping around itself”
does not exist, it does exist up to forgetting at which point in we start the wrapping,
hence the map that always exists lands in the quotient space
In general we take this to be the homotopy quotient space.
There is then the following generalization of proposition on
transmutation of coefficients under double dimensional reduction
Proposition
Let be an abelian topological group.
Then there is a weak homotopy equivalence of the form
Notice that a twisting appears. This is a general phenomenon.
We will see below that for the example of reduction of M-flux
the twist that appears is that in the twisted de Rham cohomology
which connects RR-fields with the H-flux .
Indeed this dimensional reduction is again an equivalent way of regarding the higher dimensional situation:
Proposition
(double dimensional reduction on topological flux fields)
There is a pair of adjoint functors (adjoint (∞,1)-functors really)
(a proof in more generality is below after prop. ).
Equivalently (by Nikolaus-Schreiber-Stevenson 12):
There is a pair of adjoint functors (adjoint (∞,1)-functors really)
Hence for
an -principal bundle and some coefficients,
then there is a natural equivalence
Accordingly we have the following generalization of example to the case with possibly non-trivial circle-fibration and non-trivial D0-flux:
Example
Consider naive -flux fields and on an 11d spacetime that
is an -principal bundle
Its charges is represented by a map of the form
By adjunction this is identified with a map of the form
where on the right we transmuted the coefficients by prop.
Hence the D0-brane charge appears! It is the first Chern class of the M-theory circle bundle.
Conclusion
The double dimensional reduction of any flux field
is
The operation
may be called cyclification
because the cohomology of this quotient of the free loop space
Shadows of this construction appear prominently also at other places in string theory
notably in discussion of the Witten genus.
A closely related concept in mathematics involving this is the transchromatic character map.
In fact this formalization of double dimensional reduction
works with loads of further data taken into account, such as the
differential geometry of spacetimes and the differential cohomology of
flux fields.
For the homotopy theory cognoscenti, here is the fully general statement:
Proposition
Let be any (∞,1)-topos such as
-
the classical homotopy theory on topological spaces as above
-
or better the homotopy theory of supergeometric homotopy types
and let be an ∞-group in such as
-
a topological group as above
-
or better Lie group such as the smooth circle group
then there is a pair of adjoint ∞-functors of the form
where
-
denotes the internal hom in ,
-
denotes the homotopy quotient by the conjugation
∞-action for equipped with its canonical ∞-action by left multiplication and the argument
regarded as equipped with its trivial --action.
Hence for
-
a coefficient object, such as for some differential generalized cohomology theory
then there is a natural equivalence
given by
Proof
First observe that the conjugation action on is the internal hom in the (∞,1)-category of -∞-actions . Under the equivalence of (∞,1)-categories
(from Nikolaus-Schreiber-Stevenson 12) then with its canonical ∞-action is and with the trivial action is .
Hence
Actually, this is the very definition of what is to mean in the first place, abstractly.
But now since the slice (∞,1)-topos is itself cartesian closed, via
it is immediate that there is the following sequence of natural equivalences
Here denotes the terminal morphism and denotes the base change along it.
We now apply this general mechanism to the brane bouquet.
On super -brane cocycles
By the discussion of rational homotopy theory above
we may think of L-∞ algebras as rational topological spaces
and more generally as rational parameterized spectra.
For instance above we found that the coefficient space
for RR-fields in rational twisted K-theory is the
Hence in order to apply double dimensional reduction
we now specialize the above formalization to
cyclification of super L-∞ algebras (FSS 16b)
Definition
For any super L-∞ algebra of finite type, its cyclification
is defined by having Chevalley-Eilenberg algebra of the form
where
is a copy of with cohomological degrees shifted down by one, and where is a new generator in degree 2.
The differential is given for by
where on the right we are extendng as a graded derivation.
Define
in the same way, but with .
For every there is a homotopy fiber sequence
which hence exhibits as the homotopy quotient of by an -action.
The following says that the -cyclification from prop.
indeed does model correspond to the topological cyclification from prop. .
Proposition
(Vigué-Sullivan 76, Vigué-Burghelea 85)
If
is the -algebra associated by rational homotopy theory to a simply connected topological space , then
corresponds to the free loop space of and
corresponds to the homotopy quotient of the free loop space by the circle group action which rotates the loops.
The cochain cohomology of the Chevalley-Eilenberg algebra
computes the cyclic cohomology of with coefficients in .
(Whence “cyclification”.)
Moreover the homotopy fiber sequence of the cyclification corresponds to that of the free loop space:
The following gives the super--theoretic formalization
of “double dimensional reduction”
by which both the spacetime dimension is reduced
while at the same time the brane dimension
reduces (if wrapping the reduced dimension).
We have the following -algebraic incarnation
of the general double dimensional reduction isomorphism prop. , prop. :
Proposition
(Fiorenza-Sati-Schreiber 16b, prop. 3.5)
For
a central extension of super Lie-∞ algebras, then the operation
of sending a super -homomorphsm of the form
to the composite
produces a natural bijection
between super -homomorphisms out of the exteded super -algebra
and homomorphism out of the base into the cyclification of the original coefficients
with the latter constrained so that
the canonical 2-cocycle on the cyclification is taken to the 2-cocycle classifying the given extension.
Example
Let
be the extension of a super Minkowski spacetime from dimension to dimension .
Let moreover
be the line Lie (p+3)-algebra
and consider any super (p+1)-brane cocycle from the old brane scan in dimension
Then the cyclification of the coefficients (prop. ) is
and the dimensionally reduced cocycle
has the following components
It follows that with
also
This is the dimensional reduction observed in the old brane scan (Achúcarro-Evans-Townsend-Wiltshire 87)
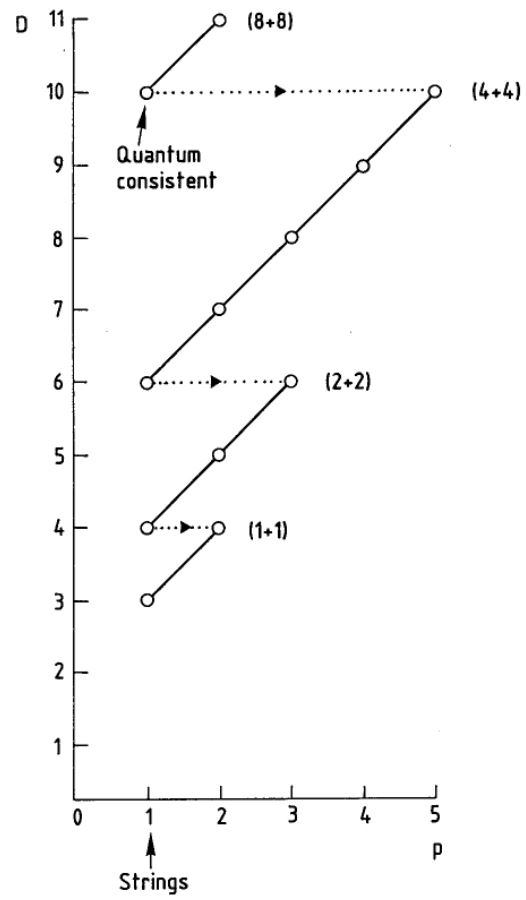
graphics grabbed from (Duff 87)
But there is more: the un-wrapped component of the dimensionally reduced cocycle satisfies the twisted cocycle condition
These relations are not to be ignored.
This we turn to now.
Dualities
We discuss now how
by repeatedly applying
the super -algebraic dimensional reduction/oxidation isomorphism of prop.
to the descended cocycles (above) from the brane bouquet
yields super -algebraic equivalences
that reflect the pertinent dualities in string theory
-
between M-theory and type IIA string theory by KK-compactification
-
between type IIA string theory and type IIB string theory (T-duality)
-
between type IIB string theory and itself (S-duality)
-
between type IIB string theory and F-theory.
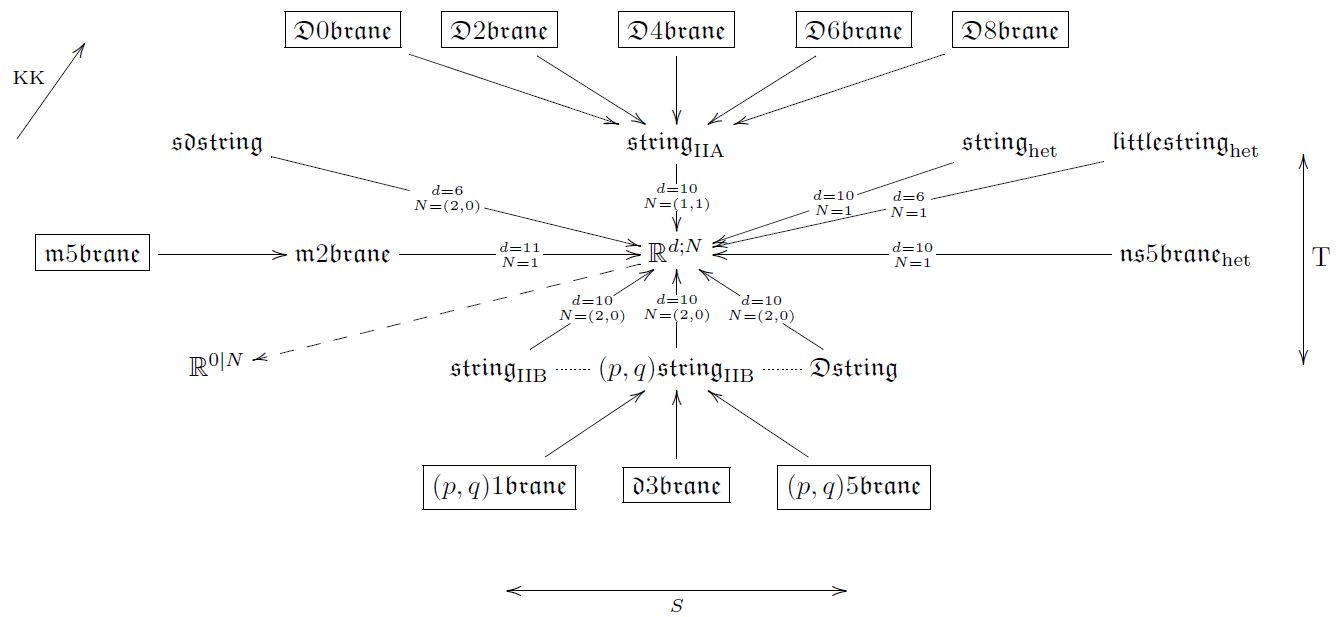
We now discuss each aspect of this picture.
M/IIA-Duality via Double dimensional reduction via Cyclification
is all controled by the following Fierz identities
for the Majorana spin representation for
and
(D’Auria-Fré 82b (3.13) and (3.28))
The first Fierz identity says that
is a 4-cocycle on , classifying the
supergravity Lie 3-algebra extension
The second says that
is a 7-cocycle on
Equivalently, (by the discussion at M-Flux fields above)
with the rational 4-sphere
then the two Fierz identities together say that there is a single 4-sphere valued cocycle
Hence is the rational coefficient for the unified M2/M5 M-flux fields.
Now we compute what becomes of this under double dimensional reduction via -cyclification (prop. )
Proposition
(Fiorenza-Sati-Schreiber 16a, section 3)
The cyclification of the M-brane coefficient
is the truncated IIA F1/D-brane coefficient
with an extra twist for the NS5-brane:
Under this identification
the -theoretic dimensional reduction according to prop.
of the unified M-brane cocycle of prop.
Observe that (by adjunction) this double dimensional reduction operation
is an isomorphism, hence
- the M2/M5-brane cocycle in 11d
is equivalent to
- the F1/D/NS5-brane cocycle
Hence this is the M/IIA duality
on super -brane super Lie -algebra cocycles.
IIA/IIB-Duality via T-Duality
The archetypical duality in string theory is T-duality, which relates the F1/Dp/NS5-super p-branes of type IIA string theory on a superspacetime which is a circle fiber bundle over a 9d base to those of type IIB string theory on a dual circle fibration with the fiber size inverted in string length units. The F1/Dp-super p-brane charges on both sides of this duality take values in twisted K-theory, and hence the mathematical statement here is that dual circle fibrations of this form induce an equivalence in twisted K-theory. This T-duality equivalence of F1/D-brane charges in twisted K-theory is known in the literature as “topological T-duality”.
The IIA and the IIB spacetime both extend the single 9d spacetime
Apply double dimensional reduction of the unified -cocycles
in IIA and IIB along both of these.
The resulting cyclified -cocycles in 9d turn out to be -equivalent.
One derives the following picture
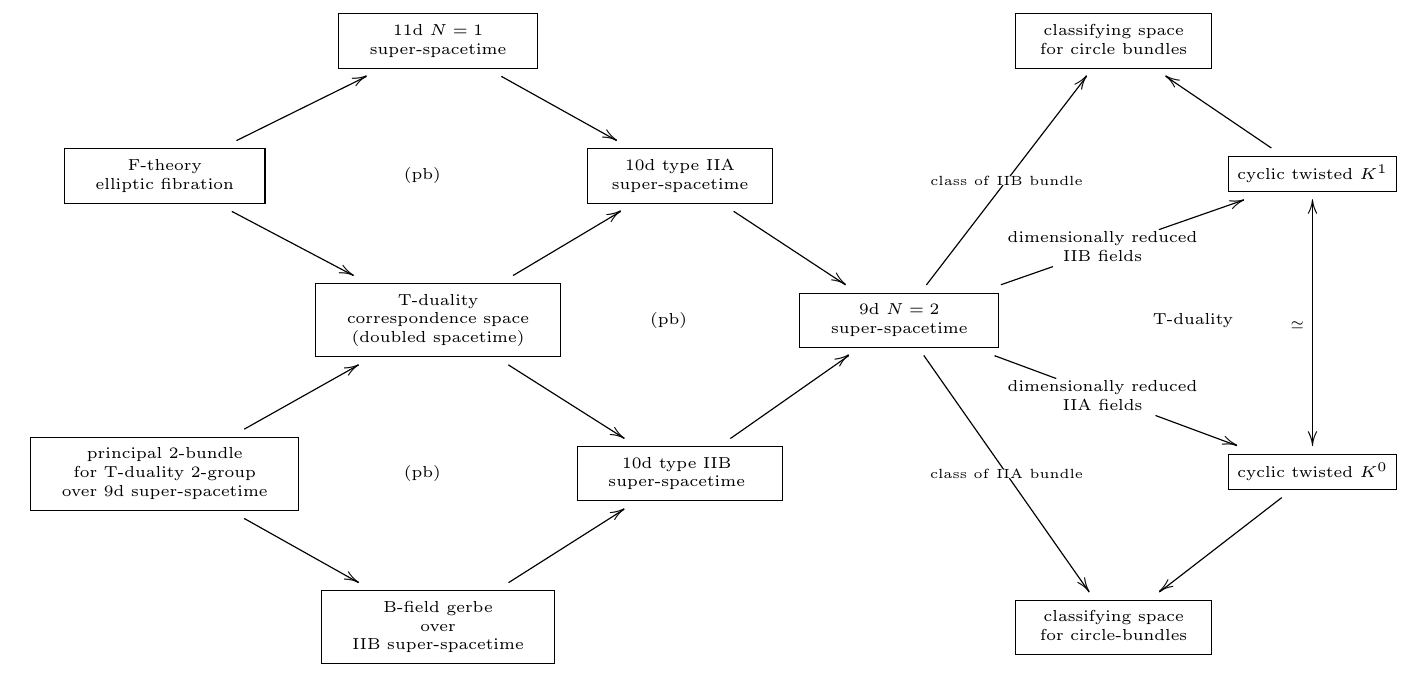
(…)
IIB/F
(…)
(…)
References
Detailed pointers to the literature are contained in the above text.
Here we only list the references to the original work reported on here.
The bosonic string Lie 2-algebra is discussed in the appendix of
- John Baez, Alissa Crans, Urs Schreiber, Danny Stevenson, From loop groups to 2-groups, Homology Homotopy Appl. Volume 9, Number 2 (2007), 101-135. (arXiv:math/0504123)
Its role in Green-Schwarz anomaly cancellation is discussed in
- Hisham Sati, Urs Schreiber, Jim Stasheff, Twisted Differential String and Fivebrane Structures, Communications in Mathematical Physics, Volume 315, Issue 1 (2012) (arXiv:0910.4001)
and its role in the flux quantization of the supergravity C-field in
- Domenico Fiorenza, Hisham Sati, Urs Schreiber, The moduli 3-stack of the C-field, Communications in Mathematical Physics, Volume 333, Issue 1 (2015), Page 117-151 (arXiv:1202.2455)
and
- Domenico Fiorenza, Hisham Sati, Urs Schreiber, Multiple M5-branes, String 2-connections, and 7d nonabelian Chern-Simons theory, Advances in Theoretical and Mathematical Physics, Volume 18, Number 2 (2014) (arXiv:1201.5277)
Our discussion of L-infinity algebra cohomology is due to
- Hisham Sati, Urs Schreiber, Jim Stasheff, L-infinity algebra connections and applications to String- and Chern-Simons n-transport, in Quantum Field Theory, Birkhäuser (2009) 303-424 (arXiv:0801.3480)
The observation of the brane bouquet in super -algebra and the general construction of higher WZW terms from higher -cocycles is due to
- Domenico Fiorenza, Hisham Sati, Urs Schreiber, Super Lie n-algebra extensions, higher WZW models and super p-branes with tensor multiplet fields International Journal of Geometric Methods in Modern Physics Volume 12, Issue 02 (2015) 1550018, (arXiv:1308.5264)
The homotopy-descent of the M5-brane cocycle and of the type IIA D-brane cocycles is due to
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, The WZW term of the M5-brane and differential cohomotopy, J. Math. Phys. 56, 102301 (2015) (arXiv:1506.07557)
-
Domenico Fiorenza, Hisham Sati, Urs Schreiber, Rational sphere valued supercocycles in M-theory, Journal of Geometry and Physics, Volume 114 (2017) (arXiv:1606.03206)
The derivation of supersymmetric topological T-duality, rationally, and of the higher super Cartan geometry for super T-folds is due to
- Domenico Fiorenza, Hisham Sati, Urs Schreiber, T-Duality from super Lie n-algebra cocycles for super p-branes, ATMP 22 5 (2018) [arXiv:1611.06536]
The derivation of the process of higher invariant extensions that leads from the superpoint to 11-dimensional supergravity:
General discussion of twisted cohomology is in
- Thomas Nikolaus, Urs Schreiber, Danny Stevenson, Principal ∞-bundles – General theory, Journal of Homotopy and Related Structures, Volume 10, Issue 4 (2015) (arXiv:1207.0248)
A textbook account of much of the story is in
Last revised on February 20, 2025 at 04:35:10. See the history of this page for a list of all contributions to it.
